벡터 Vector

Intro

• 벡터의 이해

벡터

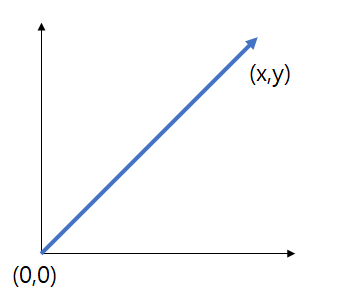
벡터(vector)는 크기 만으로 나타낼 수 있는 스칼라(scalar)와 달리 방향과 크기를 사용하여 나타낼 수 있다. 일상적으로 사용하는 벡터는 유향선분(방향이 있는 선분 즉, 화살표)를 써서 표현할 수 있다. ¹

벡터의 덧셈

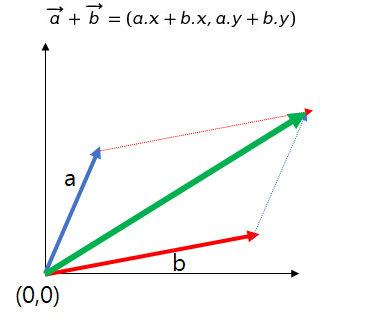
각 x,y 좌표 값을 더하면 벡터가 나온다.

시작점이 같다면 평행 사변형을 통해 구할 수 있다.

벡터의 뺄셈

벡터의 뺄셈은 뺄 벡터의 역벡터를 더해주는것과 같다.

벡터의 크기(길이)

피타고라스의 정리를 이용해 벡터의 크기(길이)를 구할 수 있다. 표기는 이중 수직선으로 표기한다.

벡터 정규화(Normalize)

Normalize(정규화)

길이를 1로 만드는 것 (순수 방향) 크기가 1인 벡터를 단위벡터(unit vector)라 부른다.

벡터의 각 성분을 벡터의 크기로 나누면 정규화 할수 있다.

벡터의 내적(Inner Product)

내적은 스칼라값을 내는 벡터 곱셈의 일종이다.

u=(u_x, u_y, u_z)이고 v=(v_x, v_y, v_z)일때 내적은 다음과 같다.

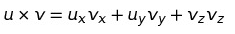
여기서 코사인 법칙을 적용해보면 다음과 같은 관계를 찾아낼 수 있다.

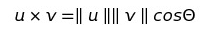
θ는 벡터 u와 v사이의 를 만족하는 각도이다. 따라서 두 벡터의 내적이 두 벡터 사이 각도의 코사인이 벡터 크기에 비례한다는 것을 뜻한다.

따라서 다음과 같은 속성을 이끌어낼 수 있다.

1. u*v = 0이면 u와 v는 직교이다.
2. u*v > 0이면 두 벡터 사이 각도 θ는 예각이다.
3. u*v < 0이면 두 벡터 사이 각도 θ는 둔각이다.

예제

u=(1,2,3)이고 v=(-4,0,-1)일때 u와 v사이 각도

uv=(1,2,3)(-4,0,-1)=-4 -3 = -7

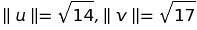
위에있는 cosθ에 대해 정리하면 각도의 근사치를 구할수 있다.

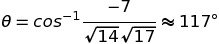
벡터의 외적(Outer Product)

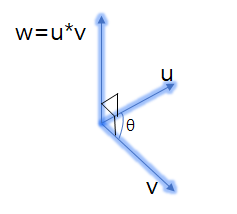
결과가 스칼라인 내적과 다르게 외적의 결과는 벡터이다. 또한 외적은 3차원 벡터에서만 정의된다. 3차원 벡터 u와 v에 외적을 하면 u와 v에 직교인 또 다른 벡터 w가 나온다.

u=(u_x, u_y, u_z)이고 v=(v_x, v_y, v_z)일 때

외적은 다음과 같다.

w=u*v=(u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)

예제

u=(2,1,3), v(2,0,0)이라고 할 때, w=uv와 z=vu를 계산하고 w가 u,v에 직교인지 확인

w=u*v

=(2,1,3)*(2,0,0)
=(1*0-3*0,3*2-2*0,2*0-1*2)
=(0,6,-2)

z=v*u

=(2,0,0)*(2,1,3)
=(0*3-0*1,0*2-2*3,2*1-0*2)
=(0,-6,2)

uv≠vu 이므로 외적은 교환법칙이 성립하지 않는다는것을 알 수 있다.

직교인지 확인하려면 내적을 이용한다.

w*u=(0,6,-2)*(2,1,3)=0*2+6*1+(-2)*3=0

w*v=(0,6,-2)*(2,0,0)=0*2+6*0,(-2)*0=0

이므로 둘다 직교이다.

유니티에서의 벡터

Vector3 a,b,c;

a=b+c;
a=b-c;
a.normalize(); (단위화)
a.magnitudue(); (길이 구하기)

참고 자료

OZTV 유튜브

프랭크 D. 루나, DirectX 12를 이용한 3D 게임 프로그래밍 입문, 한빛미디어, 2017, 3쪽

1. 위키백과 ↩