Slate

Slate

The journey is the reward.

동적 계획법 Dynamic Programming

Intro

  • 피보나치 수열을 통한 동적 계획법 이해하기

동적 계획법

복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법.

과정

문제를 여러 개의 하위문제(subproblem)으로 나누어 푼 다음 결합하여 최종 해에 도달.

하위 문제의 해를 저장한뒤 같은 하위 문제가 나올경우 간단하게 해결할 수 있다.

이러한 방법은 계산 횟수를 획기적으로 줄일 수 있다.

예제

재귀함수 형태의 피보나치 수열

#include <iostream>
using namespace std;
int fib(int n)
{
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n;
cin >> n;
cout << fib(n);
}
view raw fibonachi.cpp hosted with ❤ by GitHub

문제점

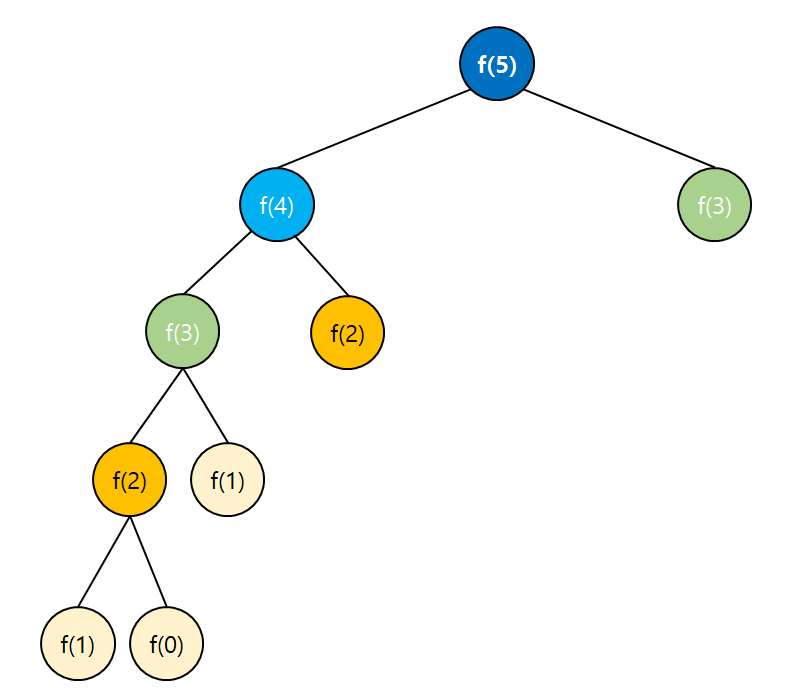
n이 커질수록 재귀트리가 많이 형성되어 계산 속도를 떨어뜨리며 오버플로우가 발생한다.

dp

fib(5)호출시 트리

동적 계획법 형태의 피보나치 수열

동적 계획법에서는 이전에 계산했던 값들을 배열에 저장해 중복계산을 막는다.

큰 문제에서 작은 문제로 분할해나가는 Top-down 방식과

작은 문제를 쌓아 큰문제를 푸는 Bottom-up방식이 있다.

Top-down 방식

#include <iostream>
using namespace std;
int memo[100] = { 0, };
int fib(int n)
{
if (n <= 1)
return n;
if (memo[n] > 0)
return memo[n];
memo[n] = fib(n - 1) + fib(n - 2);
return memo[n];
}
int main()
{
int n;
cin >> n;
cout << fib(n);
}
view raw dynamic fibo.cpp hosted with ❤ by GitHub

dp2

중복되는 값은 저장된 값을 통해 계산과정을 줄일수있다.

Bottom-up 방식

#include <iostream>
using namespace std;
int memo[100] = { 0, };
int fib(int n)
{
memo[0] = 0;
memo[1] = 1;
for (int i = 2; i <= n; i++)
{
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
}
int main()
{
int n;
cin >> n;
cout << fib(n);
}
view raw bottomup fibo.cpp hosted with ❤ by GitHub

참고자료

위키백과

댓글남기기

참고